Yisen Wang, Difan Zou, Jinfeng Yi, James Bailey, Xingjun Ma, Quanquan Gu

Shanghai Jiao Tong University, University of California, Los Angles, JD.com, The University of Melbourne

1、引言

(1) Deep neural networks (DNNs) are extremely vulnerable to adversarial examples crafted by adding small adversarial perturbations to natural examples.虽然现在深度学习网络已经在各个领域展现出优良的性能，但它被证实易受到对抗样本的攻击，我们往往可以通过在原始图片上增加一个人眼不可见的扰动使网络已较高的置信度输出一个错误的结果，考虑到对抗样本对于深度学习模型部署到现实世界中的危害（例如无人驾驶，医疗诊断等），构造良好的防御策略十分重要。

图1.对抗样本攻击网络示意图。

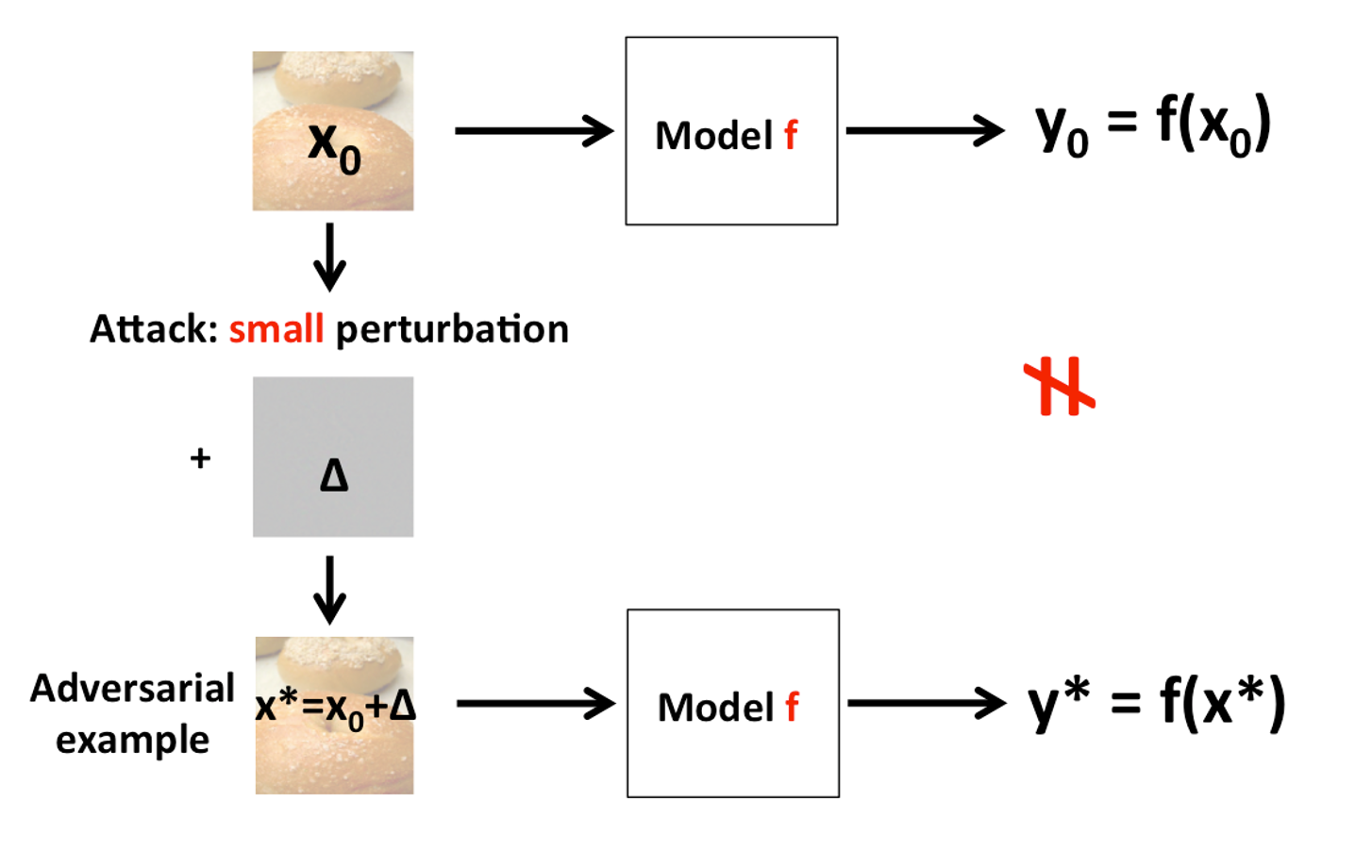
(2) 与特征压缩，输入去噪和对抗检测等前向后向处理方法相比，已提出了几种防御技术来训练DNN，这些防御方法固有地对对抗示例具有鲁棒性，包括防御蒸馏，模型压缩。 Among all the defense method, adversarial training has been demonstrated to be the most effective. Adversarial training can be regarded as a data augmentation technique that trains DNNs on adversarial examples, and can be viewed as solving the following min-max optimization problem:

\[\min_\theta \frac{1}{n} \sum_{i=1}^n \max_{||x_i^, - x_i||_p \le \epsilon} l(h_\theta(x_i^,),y_i)\]

其中$h_\theta(x_i^,)$代表网络对于对抗样本$x_i^,$的概率预测值，$y_i$是样本$x_i$的true label.

(3) 对抗训练目前存在的一些难点：

• 模型需要更大的容量。（即简单的模型可以具有很高的自然准确性，但不太可能变得更健壮）。

• 对抗训练的样本复杂度可能比自然训练高得多。

• 对抗性的鲁棒性可能天生就与自然准确性背道而驰。

(4) Recall that the formal definition of an adversarial example is conditioned on it being correctly classified. From this perspective, adversarial examples generated from misclassified examples are “undefined”. Most adversarial training variants neglect this distinction, where all training examples are treated equally in both the maximization and the minimization processes, regardless of whether or not they are correctly classified.

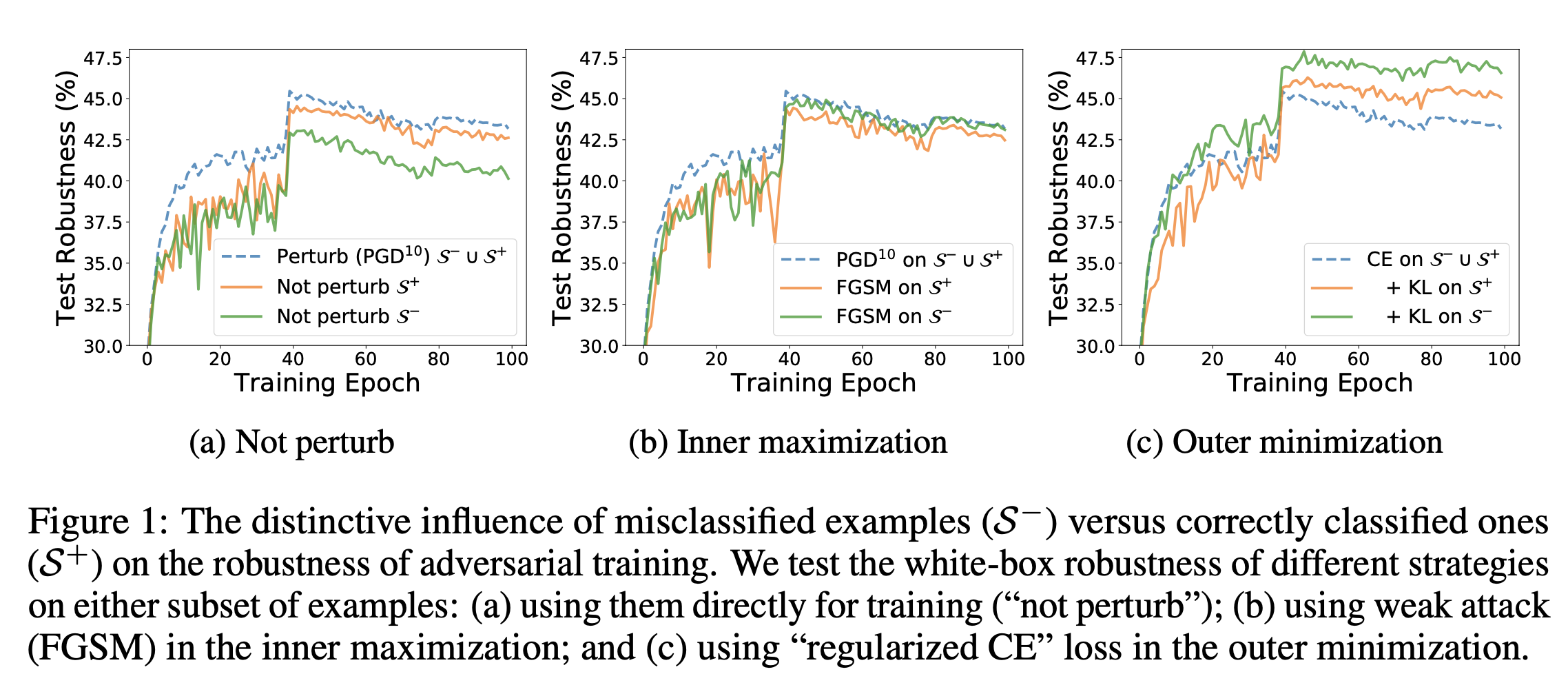
基于此，作者探索了能被原始网络正确分类的样本和不能被网络正确分类的样本对于对抗训练的差异性。把错误分类的样本记为 $\mathcal{S}^-$,把能正确分类的样本记为$\mathcal{S}^+$。

在图(a)中，作者发现分类错误的样本对最终鲁棒性有重大影响。与标准对抗训练（蓝色虚线）相比，如果在对抗训练期间未干扰子集$\mathcal{S}^-$中的样本（绿色实线），则最终鲁棒性会急剧下降（PGD仍会干扰其他示例）。相反，对子集$\mathcal{S}^+$的相同操作只会对最终的健壮性产生轻微影响（橙色实线）。先前的工作发现，删除一小部分训练示例不会降低鲁棒性，这对于正确分类的示例似乎是正确的，但对于分类错误的示例显然不是正确的。

作者应用不同的最大化技术，同时保持最小化损失CELoss不变。如图(b)所示，当使用弱攻击时（例如，快速梯度符号方法（FGSM）扰乱分类错误的样本$\mathcal{S}^-$所有训练样本仍受到PGD的干扰，最终鲁棒性几乎没有受到影响。这表明，如果内部最大化问题能够以中等精度解决，则对错误分类的样本的不同最大化技术对最终鲁棒性的影响可以忽略不计。但是，对于子集$\mathcal{S}^-$，弱化的最大化攻击往往会降低鲁棒性。

其次，作者测试了不同的最小化技术，而内在最大化仍由PGD解决。有趣的是，作者发现对错误分类的样本使用不同的最小化技术会对最终的鲁棒性产生重大影响。如图(c)所示，与带有CE损失的标准对抗训练（蓝色虚线）相比，当对错误分类的样本的外部最小化“正则化”（绿色实线）时，最终鲁棒性得到了显着改善。应用于正确分类的样本的相同正则化也有助于最终的鲁棒性（橙色实线），尽管不如错误分类的示例重要。

2、方法

2.1、误分类感知正则项（Misclassification Aware Regularization）

正确分类样本$\mathcal{S}^+$定义：

\[\mathcal{S}_{h_{\theta}}^+ = \{i:i\in [n],h_\theta(x_i)=y_i\}\]

错误分类样本$\mathcal{S}^-$定义：

\[\mathcal{S}_{h_{\theta}}^- = \{i:i\in [n],h_\theta(x_i)\ne y_i\}\]

对于错误分类样本，其对抗风险（Adversarial Risk）$\mathcal{R}^-(h_\theta,x_i)$为：

\[\mathcal{R}^-(h_\theta,x_i) :=\Bbb{1}(h_\theta(\hat{x}_i^,)\ne y_i) + \Bbb{1}(h_\theta(x_i)\ne h_\theta(\hat{x_i^,}))\]

对于正确分类样本，因为其$\Bbb{1}(h_\theta(x_i)\ne h_\theta(\hat{x_i^,}))=\Bbb{1}(h_\theta(\hat{x_i^,})=y_i)$其对抗风险（Adversarial Risk）$\mathcal{R}^+(h_\theta,x_i)$为：

\[\mathcal{R}^+(h_\theta,x_i) :=\Bbb{1}(h_\theta(\hat{x}_i^,)\ne y_i)\]

结合上述两种对抗风险，我们可以训练一个神经网络来最小化下述风险：

\[\begin{aligned} min_\theta\mathcal{R}_{misc}(h_\theta):&=\frac{1}{n}(\sum_{i\in\mathcal{S}_{h_\theta}^+}\mathcal{R}^+(h_\theta,x_i)+\sum_{i\in\mathcal{S}_{h_\theta}^-}\mathcal{R}^-(h_\theta,x_i)) \\ &=\frac{1}{n}\sum_{i=1}^n\{\Bbb{1}(h_\theta(\hat{x_i^,})\ne y_i)+\Bbb{1}(h_\theta(x_i)\ne h_\theta(\hat{x_i^,}))*\Bbb{1}(h_\theta(x_i)\ne y_i)\} \end{aligned}\] $\frac{1}{n}\sum_{i=1}^n\{\Bbb{1}(h_\theta(x_i)\ne h_\theta(\hat{x_i^,}))*\Bbb{1}(h_\theta(x_i)\ne y_i)\} $即为misclassification aware regularization。

2.2 误分类感知对抗训练（Misclassification Aware Adversarial Training(MART)）

在上一节中，我们基于0-1损失得出了误分类感知的对抗风险。但是，在实践中，超过0-1损失的优化是很困难的。接下来，通过将0-1损失替换为具有物理意义且在计算上易于处理的适当替代损失函数，提出了误分类感知训练算法（MART）。

Surrogate Loss for outer Minimization

(1) $\Bbb{1}(h_\theta(\hat{x_i^,})\ne y_i)$

作者建议使用增强型交叉熵（boosted cross entropy BCE）损失作为替代损失，而不是常用的CE损失。这主要是因为将对抗样本进行分类比自然样本需要更强的分类器，因为对抗样本的存在使分类决策边界变得更加复杂。建议的BCE损失定义为：

\[BCE(P(\hat{x}_i^,,\theta),y_i)= -log(p_{y_i}(\hat{x}_i^,,\theta))-log(1-\max_{k\ne y_i}P_k(\hat{x}_i^,,\theta))\] 其中第二项$-log(1-\max_{k\ne y_i}P_k(\hat{x}_i^,,\theta))$是用来改善分类器决策边界的margin term。

(2) $\Bbb{1}(h_\theta(x_i) \ne h_\theta(\hat{x}_i^,))$

对于第二个指标，可以用KL散度来作为替代损失函数，因为其意味着对抗样本的输出分布与原始样本不同：

\[KL(p(x_i,\theta)||p(\hat{x}_i^,,\theta))=\sum_{k=1}^K p_k(x_i,\theta)log(\frac{p_k(x_i,\theta)}{p_k(\hat{x}_i^,,\theta)})\]

(3) $\Bbb{1}(h_\theta(x_i)\ne y_i)$

第三个指标函数是强调学习错误分类样本的条件。但是，如果我们在训练过程中做出硬性决定，则无法直接优化条件。取而代之，建议使用软决策方案，将$\Bbb{1}(h_\theta(x_i)\ne y_i)$替换为输出概率$1-p_{y_i}(x_i,\theta)$。对于错误分类的示例，该值较大；对于正确分类的示例，该值较小。

Surrogate Loss for Inner Maximization

用常用的CELoss来作为替代$\Bbb{1}(h_\theta(x_i^,)\ne y_i)$函数，并用下面的式子来找到对抗样本：

\[\hat{x}_i^,=argmax_{x_i^,\in \mathcal{B}_\epsilon(x_i)}CE(p(x_i^,,\theta),y_i)\]

The overall Objective

\[\mathcal{L}^{MART}(\theta) = \frac{1}{n}\sum_{i=1}^n l(x_i,y_i,\theta)\]

其中

\[l(x_i,y_i,\theta):=BCE(p(\hat{x}_i^,,\theta),y_i)+\lambda*KL(p(x_i,\theta)||p(\hat{x}_i^,,\theta))*(1-p_{y_i}(x_i,\theta))\]

2.3 和已有工作的比较

具体地，标准算法(Standard)被设计为最小化标准对抗损失，即对抗样本上的交叉熵损失。 Logit配对方法由对抗式logit配对（ALP）和Clean Logit配对（CLP）组成，引入了一个正则化，其中包含原始样本及其对抗样本。 TRADES的目标函数还是自然损失和正则项的线性组合，这些结果对应于使用KL散度的原始样本及其对抗样本的输出概率。但是，这些算法都无法区分错误分类的样本和正确分类的样本的对于训练的差异性。

最相关的工作是MMA，它建议对正确分类的示例使用maximal margin优化，同时对误分类样本的优化保持不变。具体来说，对于正确分类的样本，MMA在对抗样本中采用交叉熵损失。对于错误分类的示例，MMA直接将交叉熵损失应用于原始样本。

MART在以下方面与MMA有所不同：

（1）MMA执行硬决策以从训练数据中识别错误分类的样本，而MART根据相应的输出概率$(p(\hat{x}^,,\theta))$，可以在培训过程中共同学习；

（2）对于正确分类的样本，MMA对具有不同扰动极限的对抗样本采用交叉熵损失，而MART在具有相同扰动极限的对抗样本上采用建议的BCE损失；

（3）对于错误分类的样本，MMA对原始样本采用交叉熵损失，而MART采用在对抗样本和原始样本上正则化的对抗损失。由于存在这些差异，稍后将在实验中证明MART优于MMA。

3、实验

3.1 Understanding the proposed MART

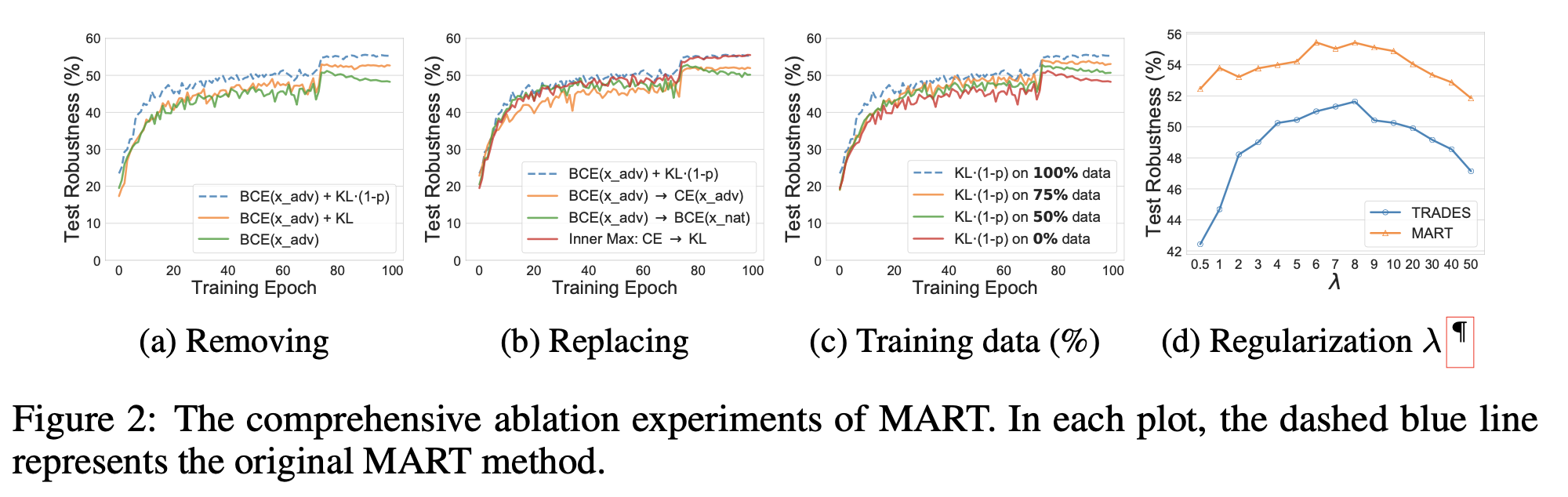
Removing Components of MART

回顾MART的目标函数，它具有三个损失函数部分：BCE，KL和1-p。如图(a)所示，删除1-p或者KL或全部删除都会导致鲁棒性显著降低。特别是，我们发现软决策项1-p在整个训练过程中都具有不断提高的鲁棒性，而KL项可以帮助减轻训练的后期的过度拟合。 当两个项组合在一起时，它们会大大提高最终的鲁棒性，而不会导致过拟合。

Replacing Components of MART

如图(b)所示，当BCE组件被CE替换或在原始样本上重新定义时，最终的鲁棒性将大大降低。这表明，在整个训练过程中，使用CE而不是我们建议的BCE进行学习会导致学习不足，且鲁棒性较低。另一方面，在原始样本上使用BCE学习会在后期出现严重的过度拟合（实线）。在对抗性最小-最大框架的内部最大化（红色实线）中，当用KL代替CE时，我们没有观察到任何提升。

Ablation on Training Data

在这里，展示了我们提出的关于误分类的正则化规则对最终鲁棒性的训练数据的贡献。具体来说，我们逐渐增加使用建议的误分类感知正则化术语进行训练的训练样本的比例，并在图(c)中显示相应的鲁棒性。 使用提议的正则化的训练样本是随机选择的，并且BCE仍在所有训练（对抗）样本中定义。 可以看出，当将建议的正则化应用于更多数据时，鲁棒性可以稳定提高。 这验证了区分正确分类和错误分类的示例的好处。

Sensitivity to Regularization Parameter $\lambda$

进一步研究MART目标函数中的参数$\lambda$，该参数控制正则化的强度。我们还测试了TRADES的正则化参数$\lambda$。在图(d)中给出了不同$\lambda \in [1/2,50]$的结果。 通过显式区分错误分类和正确分类的示例，MART在$\lambda$的不同选择上均实现了良好的稳定性和鲁棒性，并且始终比TRADES更好，更稳定。

3.2 鲁棒性评估和分析

白盒攻击防御效果

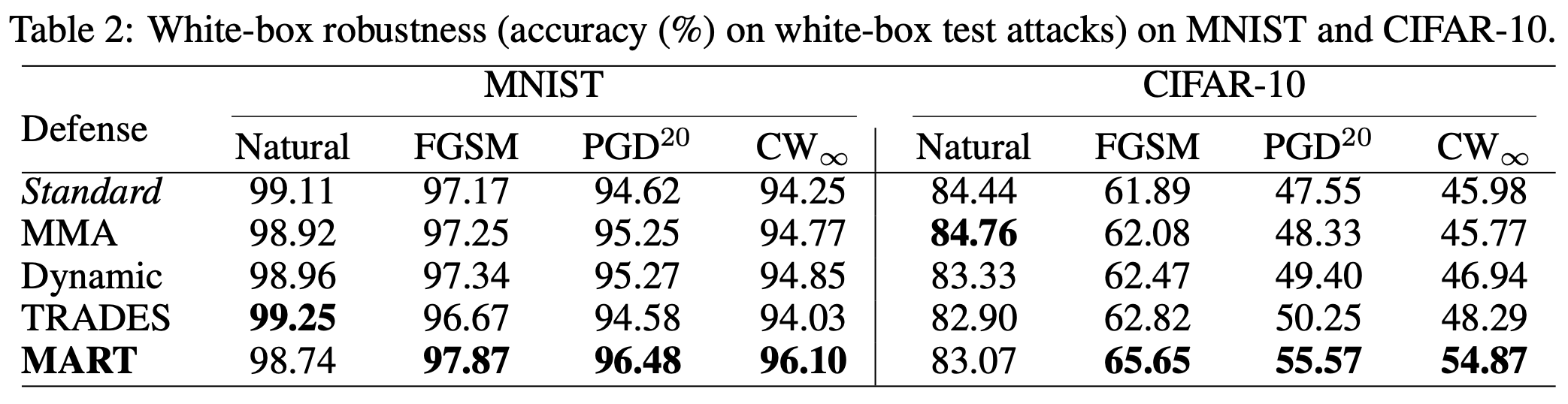
黑盒攻击防御效果

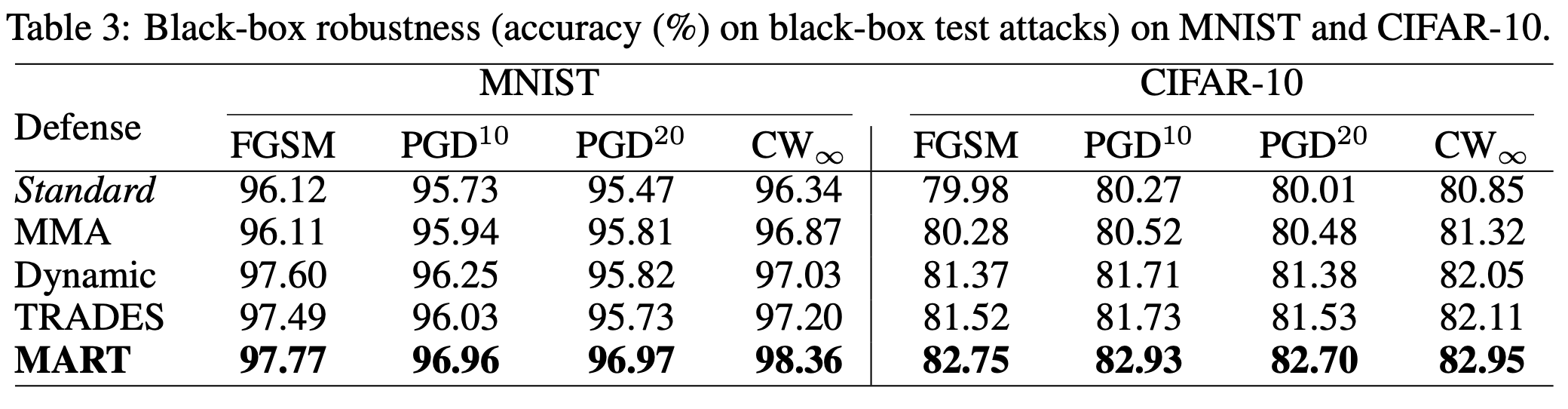
在大网络模型上效果

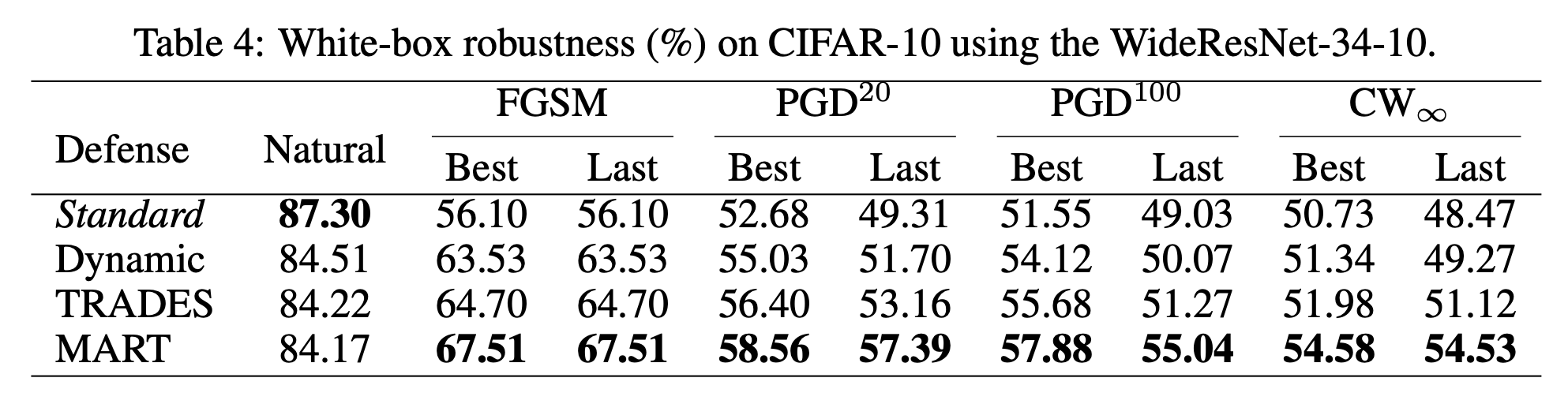
4、总结

在本文中，作者调查了一个有趣的观察，即错误分类的样本对对抗训练的最终鲁棒性具有可识别的影响，特别是对于外部最小化过程。 基于此观察，作者设计了一个误分类感知的对抗风险，其公式为在标准对抗风险中添加了误分类感知正则化。遵循常规的对抗风险，作者提出了一种新的防御算法，称为误分类感知对抗训练（MART），具有适当的替代损失函数。实验结果表明，相对于最新技术，MART可以显著提高对抗鲁棒性，并且还可以使用其他未标记数据获得更好的鲁棒性。 未来，计划在最近提出的经过认证/可证明的鲁棒性框架（Certified Robustness）中研究区分正确分类/分类错误的训练样本的影响，并探索可能带来的改进训练的差异化。

---