1.关于 Lipschitz constraint
关于深度学习中Lipschitz约束的一些性质与推导与应用在这篇博客中介绍的很清楚。
2.论文简析
2.1 解决的问题
确定了能够攻击网络的扰动的最小值,提出了一个有效的训练模型的方法来使模型鲁棒并扩大了数据点的鲁棒半径。
2.2 动机
对抗扰动的存在说明在数据点周围损失函数的斜率是很大的,所以希望限制这个斜率的bound,但是在一个input处根据损失函数求梯度会导致产生一种错误的安全感(不太懂这里的安全指的是什么意思,文章这里引了参考文献)。
因此,作者去求梯度的上界。候选方法是计算局部Lipschitz常数,即每个数据点周围的梯度的最大大小。即使可以提供证明,但计算Lipschitz常数在计算上也很困难。只能在小型网络中获得它或获得它的近似值,而后者无法提供certification。较粗略但可用的替代方法是计算全局Lipschitz常数。但是,即使对于小型网络,目前的工作也只能提供较小数量的certification。作者证明,通过改进和统一的bound以及完善的训练过程,可以克服这种缺点。训练过程比以前的方法更通用,更有效。该训练过程还可以提高针对当前攻击方法的鲁棒性。
2.3 定义
(1)防御目标
文章针对 $L_2-norm$ attack: \(\forall \epsilon, \left(||\epsilon||_2 \lt c \Rightarrow t_X = \mathop {argmax}_{i \in \{1,...,k\}} \{F(X+\epsilon)_i\}\right)\)
其中,$\epsilon$为添加的扰动大小,$c$为最大扰动约束,$t_X$为true label,该式意义在于表明,如果模型对约束在一定范围内的扰动鲁棒,则该模型输出正确的结果。
(2)Lipschitz 约束
\[||F(x)-F(x+\epsilon)||_2 \le L_F||\epsilon||_2\]其中,$L_F$为Lipschitz常数。
(3)鲁棒区域(guarded area)
用预测得分结果差作为鲁棒区域,
Prediction Margin:
\[M_{F,X} = F(X)_{t_X} - \max_{i \ne t_X} \{ F(X)_i\}\] 表示X的 true label 和模型 F 输出最大其他类别之间的“距离”。(4)鲁棒性检验约束条件
\[(M_{F,X} \ge \sqrt 2 L_F ||\epsilon||_2 ) \Rightarrow (M_{F,X+\epsilon} \ge 0)\] 所以要使得扰动不能欺骗网络,则扰动大小要小于 $M_{F,X}/(\sqrt 2 L_F)$。2.4 LMT 训练
考虑到
\[\forall i \ne t_X, (F_{t_X} \ge F_i + \sqrt2 c L_F )\]为了增大可证明的鲁棒区域范围,在每一个 $F_i$ 输出中增加 $ \sqrt2 c L_F $ 修改损失函数,训练过程中用计算近似的 $L_F$ 上界来代替$L_F$。
(1) Lipschitz上界计算
作者bound每个component(Linear Layer,Pooling and activation)的Lipschitz常数,然后递归计算overall bound。先前的工作需要对稍有不同的component进行单独分析,该论文提供了更为unified的分析。此外,该工作为求Lipschitz上界及其可微近似提供了一种快速计算算法。
这边每个component具体的Lipschitz常数计算没有怎么看懂,涉及到一些数学知识,作者提出的快速计算算法也基于在进行Lipschitz常数计算中常用的幂迭代。(2)组合
通过使用前面各component的Lipschitz bound 进行递归计算,可以相对于网络参数以可微分的方式计算整个网络的Lipschitz常数的上限。 在inference time,仅需计算一次Lipschitz常数。
在训练时的计算中,Lipschitz常数可能存在一些显着差异。 例如,批归一化层中的 $\sigma_i$ 取决于其输入。但是,根据经验,作者发现,使用与inference time 相同的bound来计算Lipschitz常数可以有效地使Lipschitz常数归一化。这样就可以处理批归一化层,尽管它对Lipschitz常数有影响,但先前的工作却忽略了。2.5 实验结果
(1)more tighter
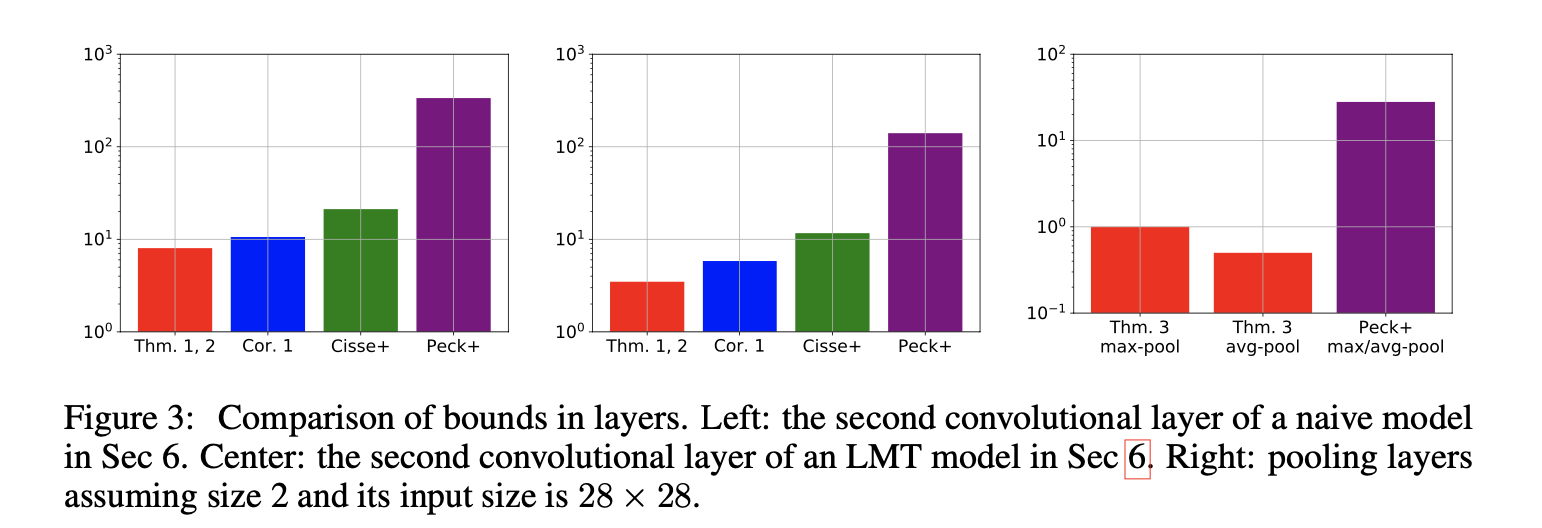
左图:在原始模型中第二个卷积层的Lipschitz bound,中间:在用LMT训练后的模型中第二个卷积层的Lipschitz bound,右图:不同pooling 层的Lipschitz bound。比较前两个子图,可以发现,经过LMT训练的模型每个component都有改进,这导致整个网络的Lipschitz常数的上界存在显着差异(具有更紧的bound)。
* analysis of tightness
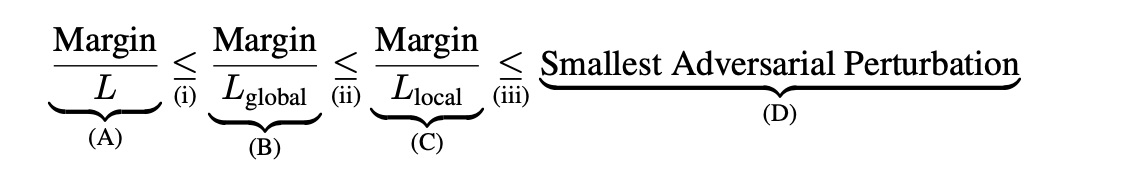
令$L$为通过该论文计算的Lipschitz常数的上界。$L_{local},L_{global}$为局部和全局Lipschitz常数。则根据Lipschitz约束条件,可以很容易得到上式。
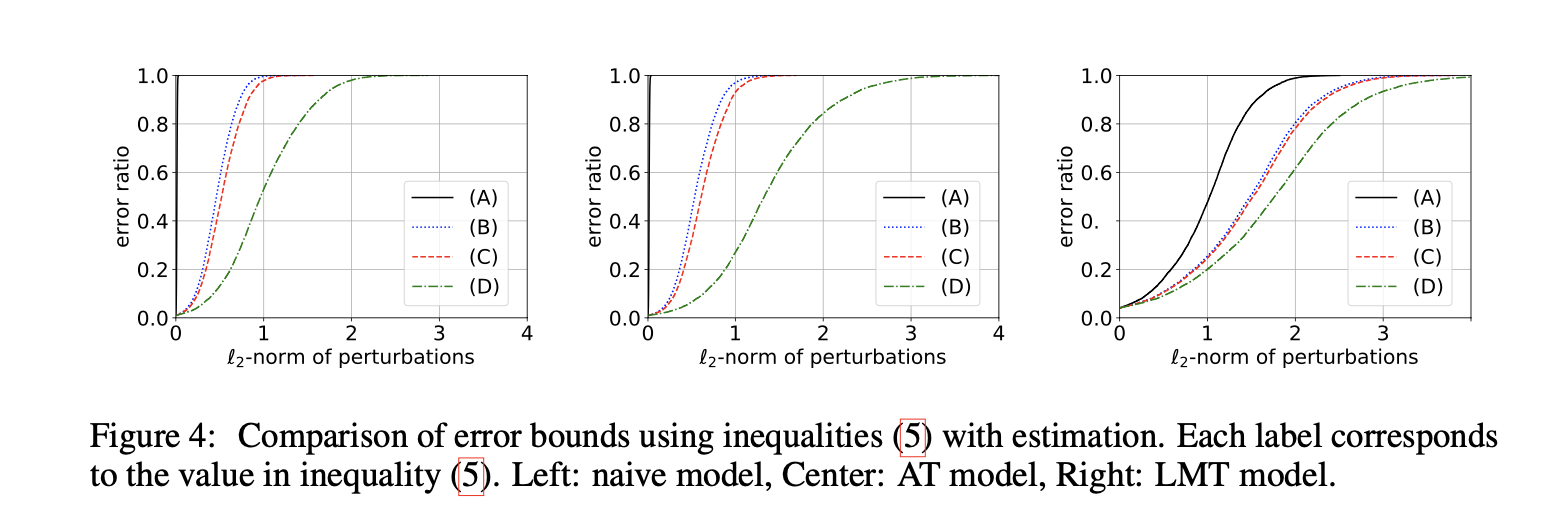
该图显示了结果。对于没有正则化的模型,(i)-(iii)中的估计错误率分别为39.9、1.13和1.82(怎么根据图得出来的,还是不根据图?)。这表明,即使我们可以用可能相当大的计算成本为每个数据点精确计算局部Lipschitz常数,不等式(iii)也会比DeepFool发现的对抗性扰动的大小松散1.8倍以上。
在AT模型中,差异超过2.4。
另一方面,在LMT模型中,(i)-(iii)中的估计错误率分别为1.42、1.02和1.15。发现的对抗性扰动的大小与可证明的鲁棒区域之间的总体中位数误差为1.72。
这表明当我们使用LMT时,受过训练的网络变得平滑,并且基于Lipschitz常数的认证变得更加严格。这也导致更好的防御攻击能力。例如,对于非正则化模型,发现的对抗性扰动的中值为0.97,而在LMT模型中,可证明的鲁棒区域区域大小的中值为1.02。
(2)Enlarge guarded area
对于使用LMT训练的模型,对于一半以上的测试数据,可以确保鲁棒区域大于0.029。以前的工作仅在小型网络中提供了此证明。
LMT与其他方法之间主要有两个区别。首先,LMT扩大了prediction margin。其次,LMT对批量归一化层进行正则化,而在其他方法中,批量归一化层则取消权重矩阵和卷积层核的正则化。作者还进行了其他实验,以提供对该网络的进一步认证。首先,将卷积替换为内核大小1,将步幅2替换为大小为2的平均池,并将卷积替换为内核大小1。然后,使用$c=0.1$的LMT。结果,尽管准确性下降到86%,但可证明的鲁棒区域的中值大于0.08。这对应于在通常的图像比例(0–255)中将400个输入元素更改为±1不会导致训练网络的误差超过50%。这些认证是不平凡的,据所知,这是为此大型网络提供的最佳认证。
(3)抵御攻击性能
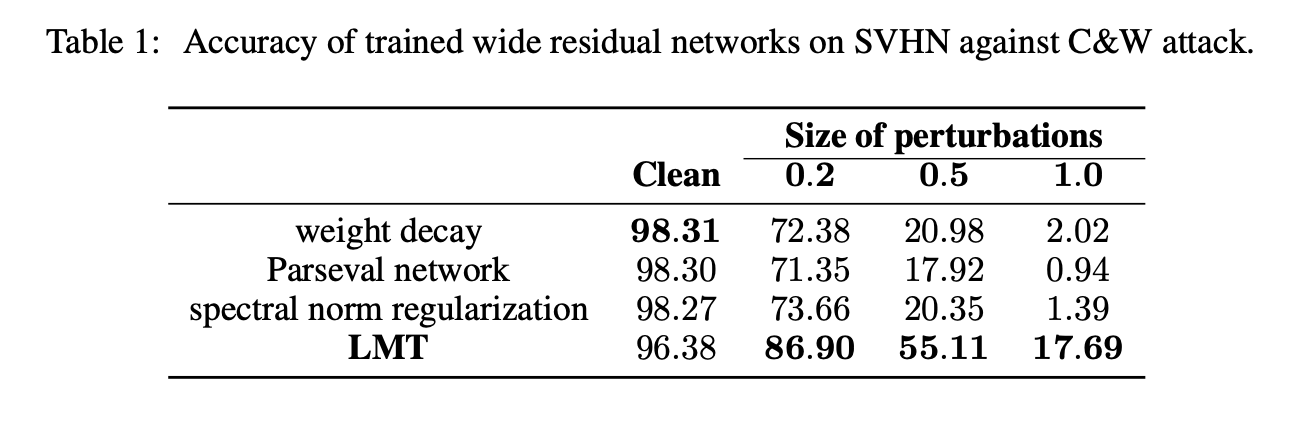
2.6 结论
为了以有效的计算过程确保广泛网络的扰动不变性,作者实现了以下目标。
1.为神经网络的每个component(Linear,pooling,activation)提供了一般的和更紧的谱范数。
2.介绍了算子范数上限及其可微近似的通用快速算法。
3.提出了一种训练算法,可以有效地限制网络的平滑性,并获得更好的认证和针对攻击的鲁棒性。
4.成功地为小型到大型网络提供了重要的认证,而计算成本却可以忽略不计。
作者相信,这项工作将成为朝着可认证且强大的深度学习模型迈出的重要一步。 将开发的技术应用于其他Lipschitz相关领域,例如GAN训练或带有嘈杂标签的训练,是未来的工作。
Reference
[1]https://papers.nips.cc/paper/7889-lipschitz-margin-training-scalable-certification-of-perturbation-invariance-for-deep-neural-networks.pdf
如果你觉得本文对你有帮助,不妨请我喝杯咖啡

