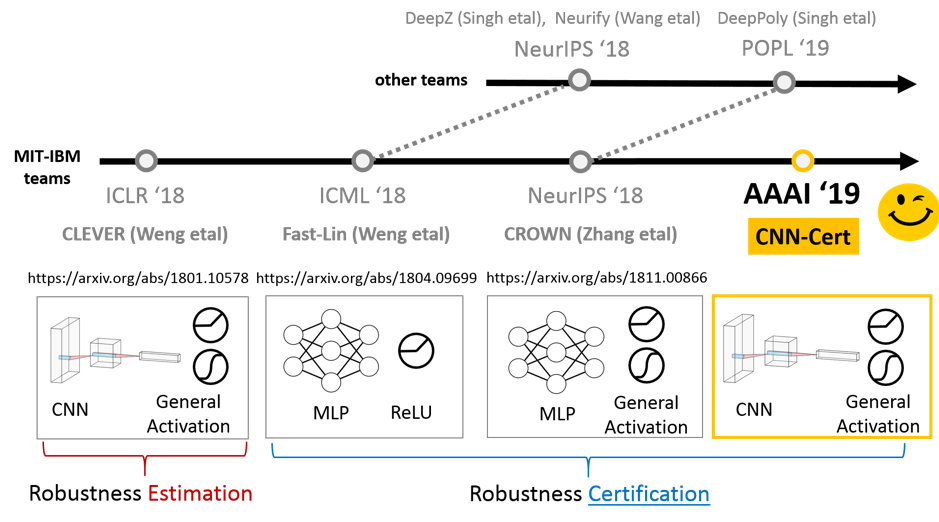
在这篇博客中,简要回顾了有关评估神经网络的鲁棒性及其研究进展的一些论文,重点是由MIT-IBM团队完成的工作。该研究进展如图1所示。然后,沿着这条线介绍了MIT-IBM实验室的四个贡献:第一个鲁棒性评估得分CLEVER,和三个鲁棒性下界认证算法,Fast-Lin和Fast-Lip用于包含ReLU激活的神经网络,CROWN用于具有通用激活的神经网络,而CNN-Cert用于通用卷积神经网络(CNN)体系结构。
1、引言
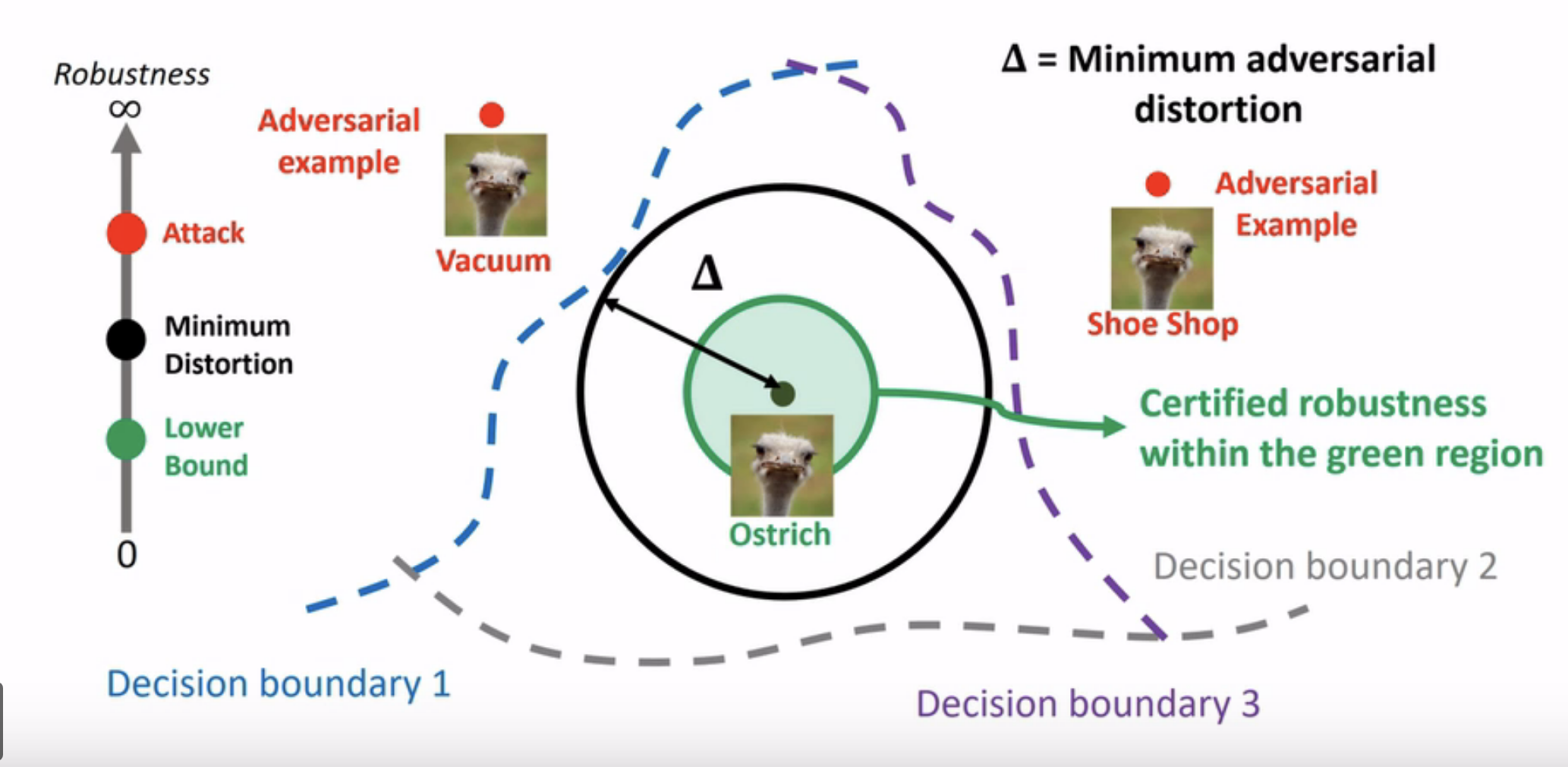
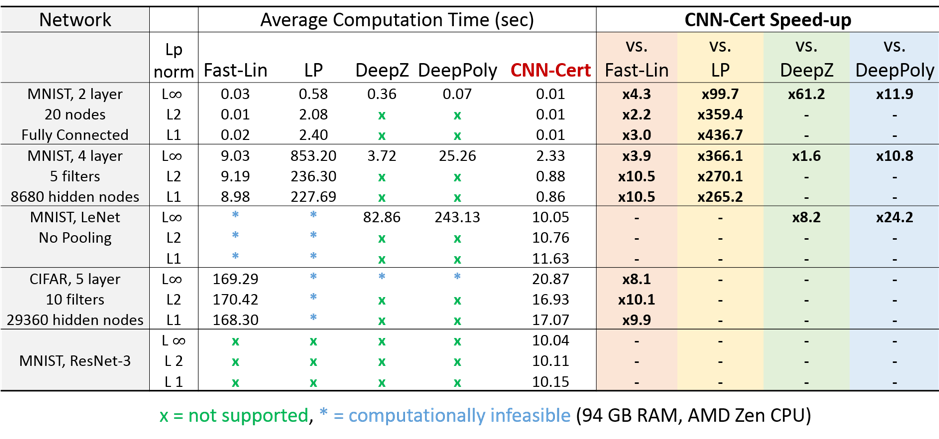
假设攻击是$L_p$范数范围的,以前的工作已经证明,为ReLU网络找到最佳的经过验证的鲁棒性在计算上是很困难的,先前的一些工作试图找到神经网络的鲁棒性的下界。此处的“鲁棒性”的概念定义为在训练过的神经网络分类器上给定测试点的最小对抗扰动,这是该研究领域的常见设置。研究人员表明,可以使用网络权重矩阵的范数约束找到鲁棒性的下界,但对于深度网络而言,这些界限通常很小。Fast-Lin为全连接网络(多层感知器)引入了非平凡的鲁棒性边界。在数学上,后来引入的DeepZ和Neurify方法提供了与Fast-Lin等效或相似的界限。接下来,CROWN方法将范围扩展到常规激活函数,并增强了ReLU网络上的范围。就方法论而言,对于仅具有卷积层的ReLU网络,CROWN和DeepPoly具有相同的公式。图2中比较了它们的数值性能。

2、Evaluating robustness of neural network with CLEVER
CLEVER及其拓展CLEVER++是发表在ICLR2018上的鲁棒性指标,以帮助评估训练有素的神经网络抵抗基于$L_p$范数的对抗攻击的鲁棒性。CLEVER具有基于分类器模型$f$的Lipschitz连续性的理论基础,并且可扩展到最新的ImageNet神经网络分类器,例如GoogleNet,ResNet等。但是,由于使用极值理论来估计基于采样的Lipschitz常数,CLEVER得分是鲁棒性的“估计”,而不是“证明”。
2.1 该指标优点
(1)与攻击方法无关;
(2)适用于任何神经网络分类器;
(3)具有强大的理论保证;
(4)对于大型神经网络在计算上是可行的。实验表明,CLEVER得分与广泛的自然和防御网络的实用鲁棒性指标非常匹配。
2.2 实现方法:使用极值理论来近似估计基于采样的Lipschitz常数
2.2.1 定义
-
鲁棒性下界$\beta_L$: 令$\Delta_{p,min}$是输入$x_0$的最小对抗扰动,则$\beta_L \le \Delta_{p,min}$是$\Delta_{p,min}$的下界,且任意扰动$||\delta||_p \le \beta_L$都不能愚弄网络。
-
鲁棒性上界$\beta_U$: 令$\Delta_{p,min}$是输入$x_0$的最小对抗扰动,则$\beta_L \ge \Delta_{p,min}$是$\Delta_{p,min}$的上界,且存在扰动$||\delta||_p \ge \beta_L$都可以使网络输出错误的结果。
- Formal guarantee on lower bound $\beta_L$ for untargeted attack(全局Lipschitz性?):
即:
\[\beta_L = \min_{j \ne c} \frac {f_c(x_0)-f_j(x_0)}{L_q^j}\]$L_q^j$是函数$f_c(x_0)-f_j(x_0)$在$L_p$范数约束下的Lipschitz常数,${1\over p} + {1 \over q} =1$,$c$是模型输出的最大可能类。
- Formal guarantee on $\beta_L$ for untargeted attack(局部Lipschitz性?):
$L_{q,x_0}^j$是$x_0$在范围$B_p(x_0,R):=\lbrace x_0 \in R^d| \quad || x-x_0||_p \le R\rbrace$内的局部Lipschitz常数,$\delta \in B_p(0,R)$。
对于目标攻击,只需代入具体目标类$f_j(x_0)$即可。2.2.2 用极值理论求解鲁棒下界问题
计算$L_q^j$的一种方法是对$x_0$周围的球$B_p(x_0,R)$中的一组点$x^{(i)}$进行采样,并取其中$||\nabla g(x^{(i)})||_q$的最大值。但是,可能需要大量样本才能获得对$max||\nabla g(x^{(i)})||_q$的良好估计,并且估计值与真实最大值相比有多好这是无从得知的。
所以采用极值理论可确保随机变量的最大值只能遵循三个极值分布之一,这对于仅用少量样本估计$max||\nabla g(x^{(i)})||_q$很有用。
- 极值理论(Fisher-Tippett-Gnedenko Theorem): 如果存在一系列实数对$(a_n,b_n)$,使得$a_n \gt 0$且$\lim_{n \rightarrow \infty} F_Y^n(a_ny+b_n)=G(y)$,其中$G$是non-degenerate分布函数,则$G$属于Gumbel类别(I型),Fréchet类别(II型)或Reverse Weibull类别(III型),其CDF如下: \(\begin{aligned} & Gumbel class(Type I): G(y)=exp\{-exp[- \frac {y-a_W}{b_W}]\}, y \in R, \\ &Fréchet class(Type II):G(y)= \begin{cases} 0, & y \lt a_W, \\ exp\{-(\frac{y-a_W}{b_W})^{-c_W}\}, & y \gt a_W, \end{cases}\\ &Reverse Weibull class(Type III):G(y)= \begin{cases} exp\{-(\frac{a_W-y}{b_W})^{-c_W}\}, & y \lt a_W,\\ 1, & y \gt a_W, \end{cases} \end{aligned}\)
2.3 CLEVER SCORE Algorithm

3、Toward certifying robustness of neural networks with CROWN
CLEVER和鲁棒性认证算法之间的区别在于,鲁棒性认证算法将始终提供保证小于最小对抗扰动的证书。这促使MIT和IBM研究人员开发了神经网络鲁棒性认证算法之一CROWN,该算法在NeurIPS2018中提出。CROWN是用于在激活函数上基于线性和二次边界技术对神经网络进行认证的通用框架,CROWN比其前身Fast-Lin和类似算法(包括DeepZ和Neurify)更加灵活,因为CROWN具有自适应(非并行)激活范围并可以处理非ReLU激活,包括但不限于tanh,Sigmoid和arctan。值得注意的是,借助自适应边界功能,CROWN能够将Fast-Lin提供的鲁棒性证书在各种MNIST和CIFAR全连接网络(MLP)上提高多达20%。但是,CROWN仅限于具有完全连接层的神经网络,而在实践中,具有各种架构(例如池化层,残差块,批归一化层)的卷积神经网络更为流行和普遍。
因此,在AAAI2019上,提出了一个更通用的框架,称为CNN-Cert,以帮助量化具有各种构建基块(包括卷积层,残差块,池化层)的神经网络分类器鲁棒性水平!
4、Toward certifying robustness of general convolutional neural networks with CNN-Cert
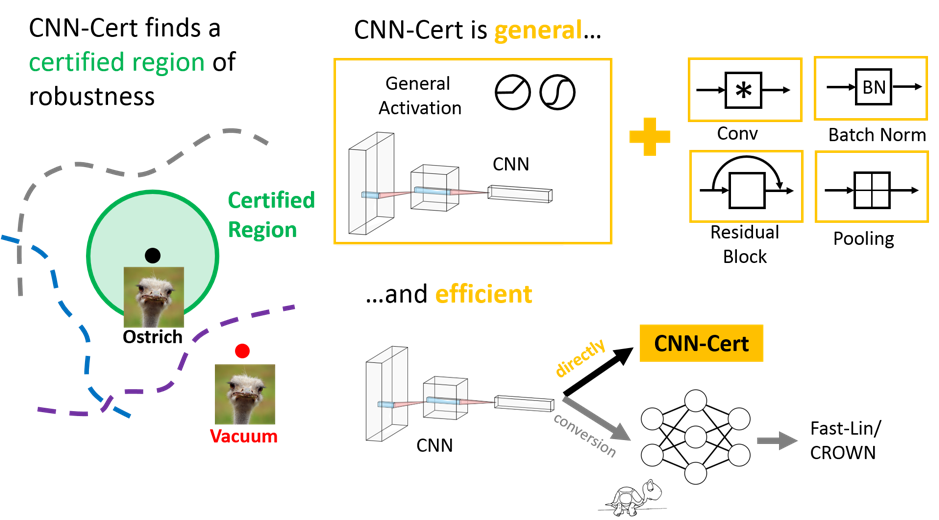
CNN-Cert的工作原理与之前的CROWN和Fast-Lin相同。基本思想是使用输入的两个线性函数上下限整个网络。这是在迭代过程中发生的:首先为第一层找到边界,然后使用先前各层的边界找到每个连续层的边界。当对抗性扰动以$L_p$范数为边界时,可以保证保持这些边界。使CNN-Cert与众不同的是,边界以卷积形式表示。也就是说,整个网络由输入的两个卷积函数上下限。对于卷积神经网络,边界的这种卷积表示的复杂度低于标准线性表示,因此比以前的方法可以更有效地计算边界。这些卷积边界可以在具有各种构造块的网络中找到,这些构造块包括但不限于卷积层,残差块,池化和批处理归一化。实际上,可以由卷积函数限制的任何构造块都可以合并到此框架中。这意味着CNN-Cert在计算上既高效又通用,如图3所示。可在此处找到再现CNN-Cert结果的代码。

4.1 定义
令$\rho_{cert}$为要求的鲁棒范围下界,
\[\forall \delta \in R^d, \|\delta\|_p \le \rho_{cert},argmax_i f_i(x_0+\delta)=c\]4.2 计算$\rho_{cert}$
我们可以利用网络输出的变化,找到最小对抗扰动的认证下限,基于这个目标,第一步是为神经网络分类器构造各种block的显式输出界限。
采用方法的基本思想是将线性边界技术分别应用于神经网络中的非线性运算,例如非线性激活函数,残差块和池化操作。
4.2.1 激活函数-卷积块
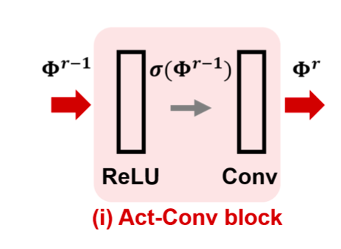
令$\Phi^r$表示该块输出,$\Phi^{r-1}$表示该块输入,则有:
\[\Phi^r = W^r *\sigma(\Phi^{r-1})\]对激活函数$\sigma(y)$实施两个线性边界约束:
\[\alpha_L(y+\beta_L) \le \sigma(y) \le \alpha_U(y+\beta_U)\]这样,可以得到每一层输出$\Phi^r$和输入$\Phi^{r-1}$之间的递推关系:
\[\begin{aligned} &\Phi^r \le A_{U,act}^r * \Phi^{r-1} + B_{U,act}^r,\\ &\Phi^r \ge A_{L,act}^r * \Phi^{r-1} + B_{L,act}^r \end{aligned}\]由此递推关系,我们可以得到输出$\Phi^r$和输入$x$之间的关系:
\[A_{L,conv}^0 * x + B_L^0 \le \Phi^r(x) \le A_{U,conv}^0 * x + B_U^0\]4.2.2 残差块
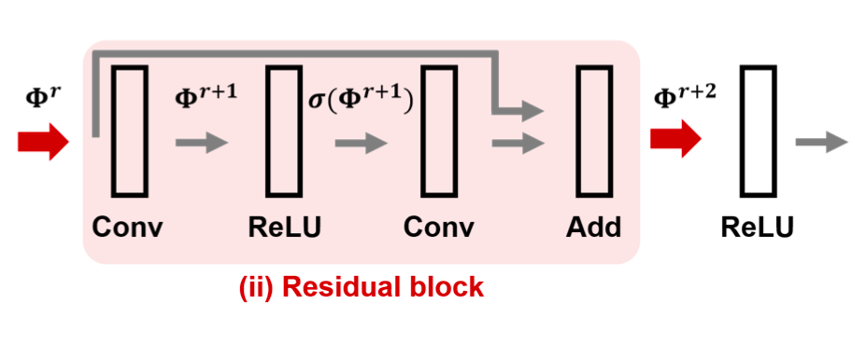
由残差块属性,对于输入输出我们有:
\[\begin{aligned} &\Phi^{r+1}=W^{r+1}*\Phi^r+b^{r+1}, \\ &\Phi^{r+2}=W^{r+2}*\sigma(\Phi^{r+1})+b^{r+2}+\Phi^r. \end{aligned}\]利用激活函数约束,我们可以得到:
\[\begin{aligned} &\Phi^{r+2}\le A_{U,res}^{r+2}*\Phi^r+B_{U,res}^{r+2},\\ &\Phi^{r+2}\le A_{L,res}^{r+2}*\Phi^r+B_{L,res}^{r+2}. \end{aligned}\]4.2.3 批归一化块
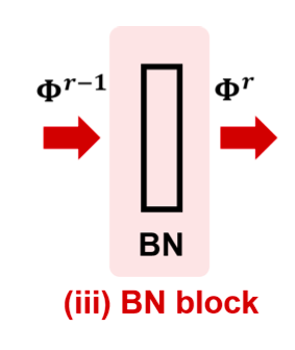
我们有:
\[\Phi^r = \gamma_{bn}{\frac {\Phi^{r-1}-\mu_{bn}}{\sqrt {\sigma_{bn}^2+\epsilon_{bn}}}}+\beta_{bn},\]可以得到:
\[A_{L,bn}^r*\Phi^{r-1}+B_{L,bn}^r \le \Phi^r\le A_{U,bn}^r * \Phi^{r-1}+B_{U,bn}^r\]4.2.4 池化块
针对最大池化,有:
\[\Phi_n^r=\max_{S_n}\Phi_{S_n}^{r-1},\]可得到递推式:
\[\begin{aligned} &\Phi^r \le A_{U,pool}^r * \Phi^{r-1}+B_{U,pool}^r,\\ &\Phi^r \ge A_{L,pool}^r * \Phi^{r-1}+B_{L,pool}^r, \end{aligned}\] 上面提到的各种$A,B$的上下界具体形式由图4给出。
4.3 全局bound形式
\[A_L^0 * x + B_L^0 \le \Phi^m(x) \le A_U^0 * x +B_U^0\]4.4 约束在$B_p(x_0,\epsilon)$范围内的全局上下界
输入$x$约束在以输入数据点$x_0$为中心且半径为$\epsilon$的$l_p$球$B_p(x_0,\epsilon)$内。因此,在$x\in B_p(x_0,\epsilon)$上最大化(最小化)上式的右侧(左侧)会导致第j个输出$\Phi_j^m(x)$的全局上限(下限):
\[\begin{aligned} &\eta_{j,U}=\epsilon\|vec(A_U^0)\|_q+A_U^0*x_0+B_U^0,\\ &\eta_{j,L}=\epsilon\|vec(A_L^0)\|_q+A_L^0*x_0+B_L^0. \end{aligned}\]4.5 确定可验证下界$\rho_{cert}$
给定最大输入扰动$\epsilon$,我们可以通过上式得到全局边界,从而来检验$\Phi_c^m(x)-\Phi_t^m(x)\gt0$是否被满足。即,给定一个$\epsilon$,我们将检查条件$\eta_{c,L}-\eta_{t,U}\gt0$,条件为真,则增加$\epsilon$,否则减少$\epsilon$。
5、工作比较
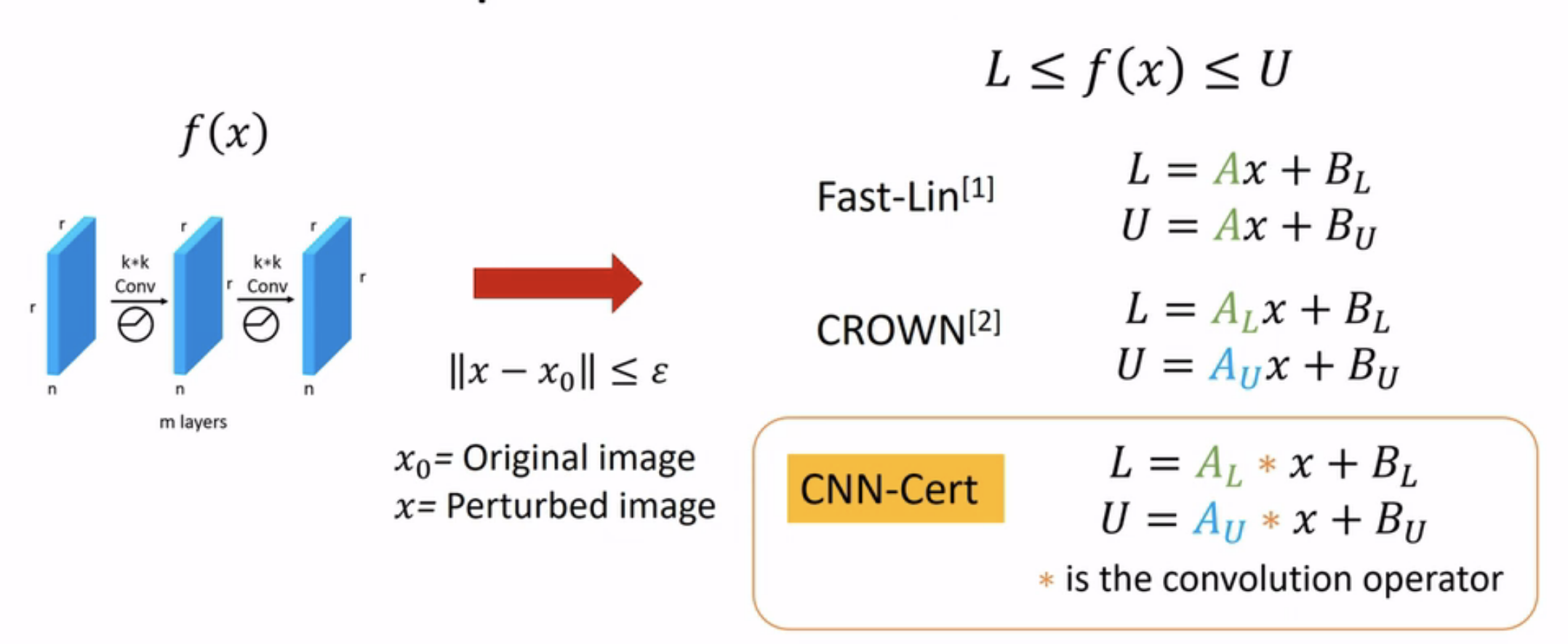
6、总结
评估和量化神经网络的鲁棒性无疑是深度神经网络最重要的研究问题之一,因为它可以帮助我们更好地了解神经网络的脆弱性,并为将来设计更鲁棒的神经网络奠定基础。 在这篇博客中,简要回顾了MIT-IBM实验室的三种鲁棒性评估和认证算法。
Reference
Robustness scores
(1) CLEVER: https://arxiv.org/abs/1801.10578
(2) CLEVER++: https://arxiv.org/abs/1810.08640
Robustness certificates
(1) Fast-Lin:https://arxiv.org/abs/1804.09699
(2) CROWN: https://arxiv.org/abs/1811.00866
(3) CNN-Cert: https://arxiv.org/abs/1811.12395
如果你觉得本文对你有帮助,不妨请我喝杯咖啡

