1、整体框架
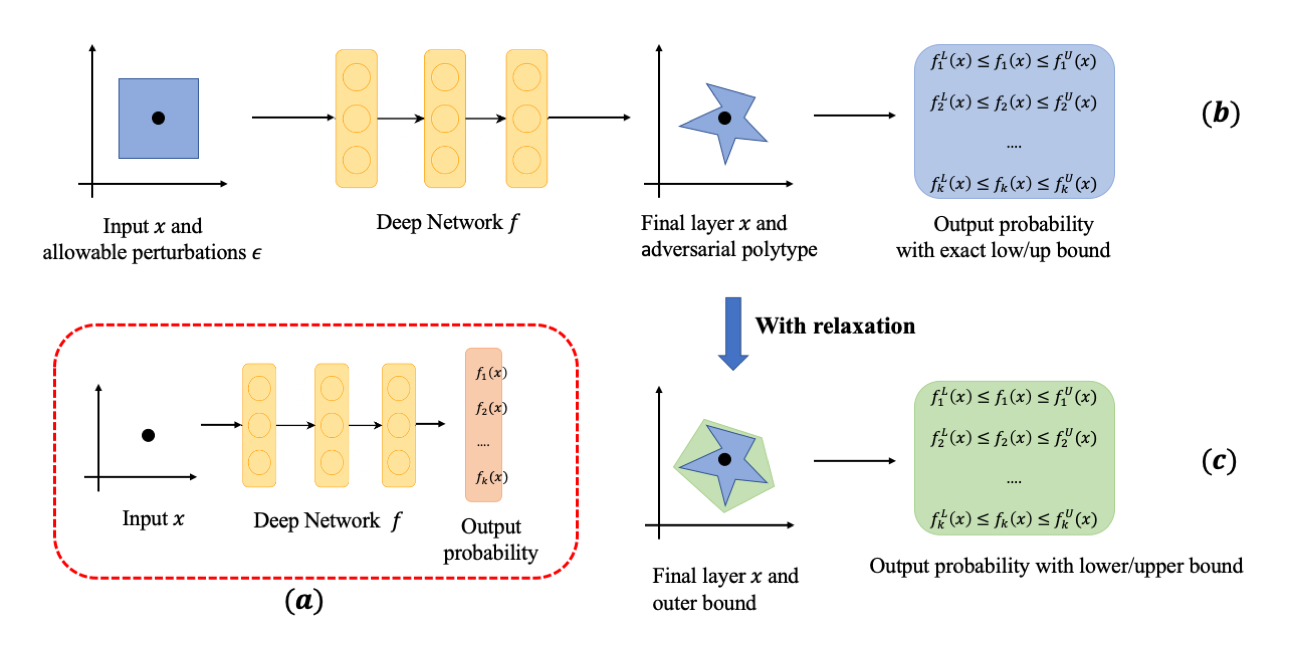
令$\lbrace x,y\rbrace_{i=1,\cdots,n}$表示原始输入数据集,$x \in R^d, y \in \lbrace 1,\cdots k \rbrace$。神经网络$f$的可验证鲁棒性评估流程如图1.1所示。
其中图1.1(a)表示神经网络对原始图片的判别过程,输入$x$,输出$x$属于每一类别的概率值$f_1(x),\cdots, f_k(x)$。
图1.1(b)表示网络$f$对给定原始图片及其周围扰动区域的精确判别过程。令$x_0$为给定的数据点,让扰动的输入向量$x$位于以$x_0$为中心,以$\epsilon$为界的$L_p$球内,即
\[x\in \mathcal{B}_p(x_0,\epsilon),\mathcal{B}_p(x_0,\epsilon):=\{x | \|x-x_0\|_p\leq \epsilon\}\]则以$\epsilon$为界的$L_p$扰动区域经过网络的传递变为一个非凸的扰动区域,在该非凸的扰动区域内存在确定的$\epsilon_{a_i,b_i}$,使网络对其的概率输出为原始给定样本的精确上下界。即
\[f_i^L(x_0) \leq f_i(x_0) \leq f_i^U(x_0), f_i^L(x_0)=f_i(x_0+\epsilon_{a_i}), f_i^U(x_0)=f_i(x_0+\epsilon_{b_i}), i \in \{1,\cdots,k\}.\]图1.1(c) 表示网络$f$对给定原始图片及其周围扰动区域的松弛判别过程。事实上,在(b)中网络最后一层的非凸扰动区域内找到确定的$\epsilon_{a,b}$是计算代价十分昂贵,所以采取在网络传递过程中通过一定的松弛策略,将非凸扰动区域松弛为一个凸扰动区域,并在该凸扰动区域内找寻$\epsilon_{a_i\prime,b_i\prime}$,使网络对其的概率输出为原始给定样本的松弛上下界。即
\[f_i^L(x_0) \leq f_i(x_0) \leq f_i^U(x_0),f_i^L(x_0)=f_i(x_0+\epsilon_{a_i\prime}), f_i^U(x_0)=f_i(x_0+\epsilon_{b_i\prime}), i \in \{1,\cdots,k\}\] \[f_i(x_0+\epsilon_{a_i\prime}) \leq f_i(x_0+\epsilon_{a_i})\leq f_i(x_0+\epsilon_{b_i}) \leq f_i(x_0+\epsilon_{b_i\prime}).\]2、验证过程
我们称模型在$x_0$点处具有可验证鲁棒性,即在扰动区域内不存在扰动可以使得模型输出错误的标签,即对于
\[\forall x \in \mathcal{B}_p(x_0,\epsilon),\mathop {argmax}_{i\in \{1,\cdots,k\}}f_i(x)=y_{true}.\]2.1 Certified exact/lower bound
设$c$是输入$x_0$的正确标签,$j$是攻击标签,则网络对于目标攻击和非目标攻击的certified bound $\hat \epsilon_j$ 和 $\hat \epsilon$可以被定义如下:
\[\hat \epsilon_j = \max_\epsilon \epsilon \quad s.t. \quad g(x,\epsilon):=f_c(x)-f_j(x) \gt 0,\quad x\in \mathcal{B}_p(x_0,\epsilon)\] \[\hat \epsilon = \min_{j \neq c} \hat \epsilon_j\]我们可以通过二分查找去得到$\hat \epsilon_j$。具体的,我们首先给定一个初始的$\epsilon$,并去计算$g(x,\epsilon)\gt 0$是否成立。如果成立,则增大$\epsilon$,否则减小$\epsilon$。
值得注意的是,通过松弛方法得到的$\hat \epsilon_j$是certified lower bound。因为它将网络最后一层扰动区域变大了。2.1 Verrfied Error
针对一个样本,如果模型存在可能被攻击的类别,则说明模型在这个样本上不鲁棒。具体的,可以通过如下定义判定模型对样本$x_0$在扰动大小为$\epsilon$情况下是否可能被攻击成功:
\[\mathcal{S}(x_0,\epsilon)_j:=f_c^L(x)-f_j^U(x), \quad x\in \mathcal{B}_p(x_0,\epsilon)\]其中,$c$是输入$x_0$的正确标签,$j$是攻击标签。如果对于$\forall j \neq c$,均有$\mathcal{S}(x,\epsilon)_j \ge 0$,则说明模型对此样本鲁棒。
Verrified error 计算公式如下:
\[Verrfied Error:=\frac{\mathbb{I}(\mathop {argmax}_{i\in \{1,\cdots,k\}}f_i(x_0)=c)\quad \&\quad \mathbb{I}(\mathcal{S}(x_0,\epsilon)_{i \neq c} \ge 0))}{n}\]其中$k$为类别数,$c$为正确标签,$n$为样本数。
通过松弛方法得到的Verrfied error比精确解大,且越松弛越大,因为它将网络最后一层扰动区域变大了,要在该扰动区域保持鲁棒性变得更不容易。3、训练优化过程
在对抗扰动下的分类任务中,针对每个目标类别$i \ne c$,我们优化最坏情况下的鲁棒边界来训练一个鲁棒的模型。具体的,我们令正确标签的输出概率等于其下界,通过约束,使其下界变大;令其他标签的输出概率等于其上界,通过约束,使其上界变小:
\[\hat f_i(x_0) = \begin{cases} f_i^U(x), & i \ne c \\ f_i^L(x), & otherwise \end{cases} x\in \mathcal{B}_p(x_0,\epsilon)\]则最后的损失函数可以表示如下:
\[L=k \ell(f(x_0),c)+(1-k)\ell(\hat f(x_0),c)\]其中$\ell$是cross-entropy损失函数,$k$为超参数。
4、现有方法
4.1 验证方法
不同松弛方法。(1)IBP(Interval Bound Propagation)
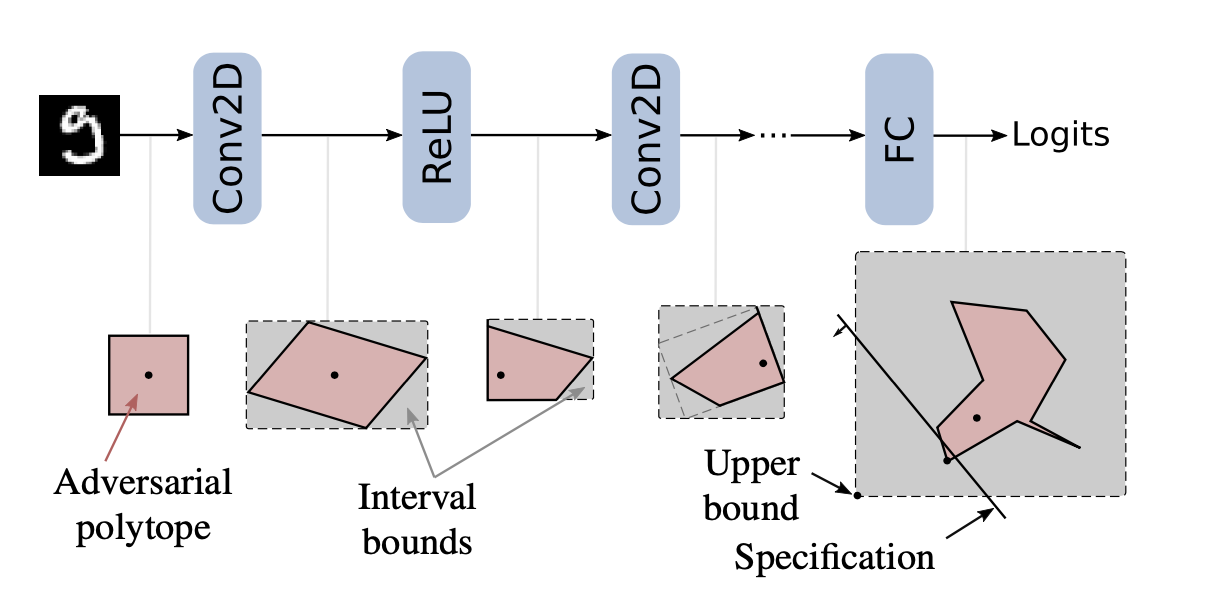
IBP方法通过一个轴对齐边界来松弛每一层输出。该方法计算快速,且能scale到大网络上,而且通过IBP计算的上下界可以用在优化过程来训练一个鲁棒的模型。
(2)Fast-Lin
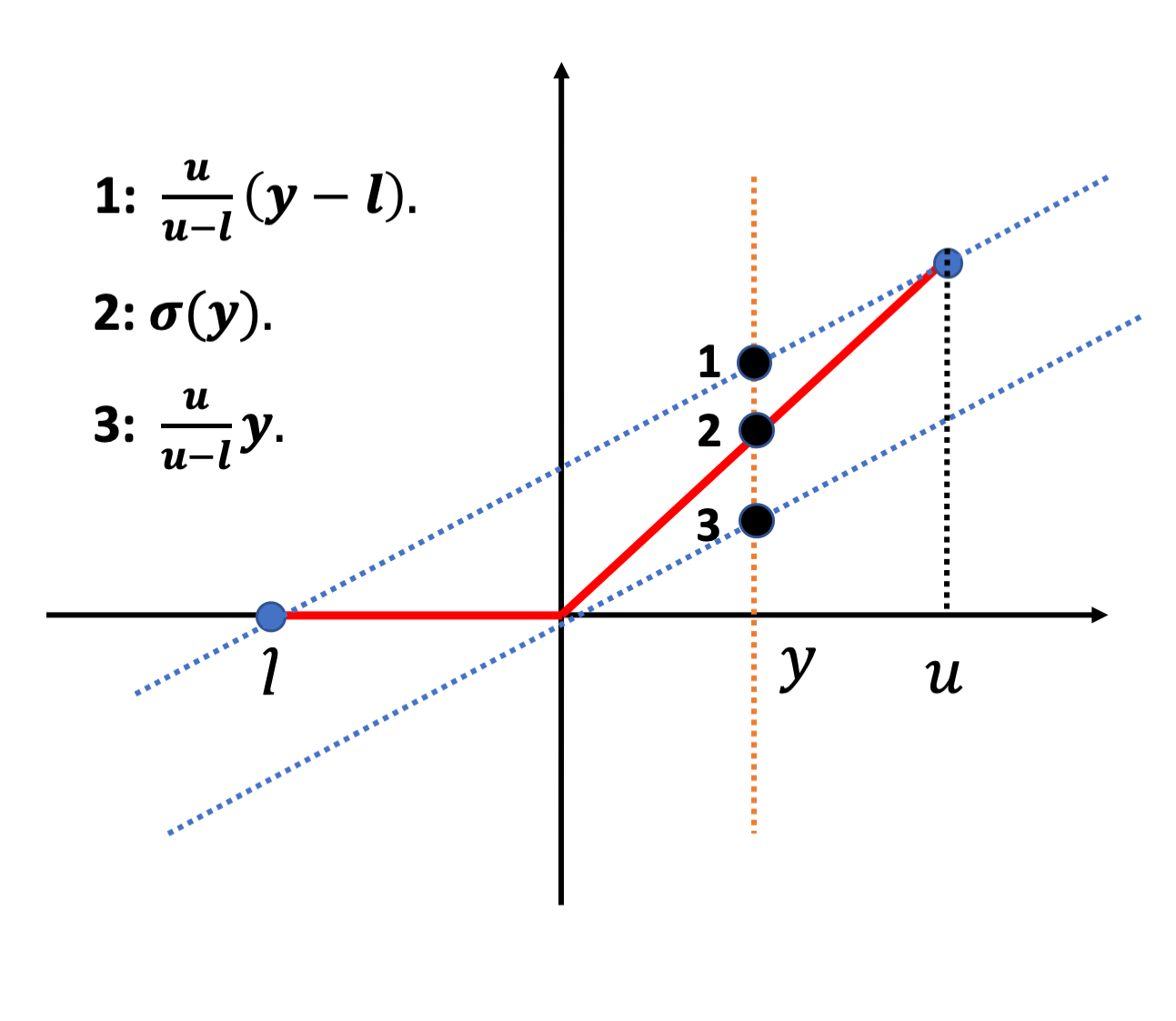
我们用如图2.1所示线性上限和线性下限来代替ReLU激活$\sigma(y)$,从而可以得到ReLU的线性松弛上下界为:
\[\frac{u}{u-l}y \leq \sigma(y) \leq \frac{u}{u-l}(y-l)\](3)Fast-Lip
Fast-Lip 通过计算$min (g(x)/L_{q,x_0}^j,\epsilon)$来计算certified lower bound。其中$g(x)=f_c(x)-f_j(x)$,$L_{q,x_0}^j$ 是$g(x)$在$\mathcal{B}_p(x_0,\epsilon)$中的局部Lipschitz常数,$j$是攻击类标,$c$是原始正确类标,$1/p+1/q=1$。而且向量的最大范数($\nabla g(x),x\in \mathcal{B}_p(x_0,\epsilon)$)以每个分量的最大值的范数为上限。 通过计算${\nabla g(x)}_k$的最坏情况模式及其范数,我们可以获得局部Lipschitz常数的上限,从而计算出鲁棒下界。
(4)CROWN
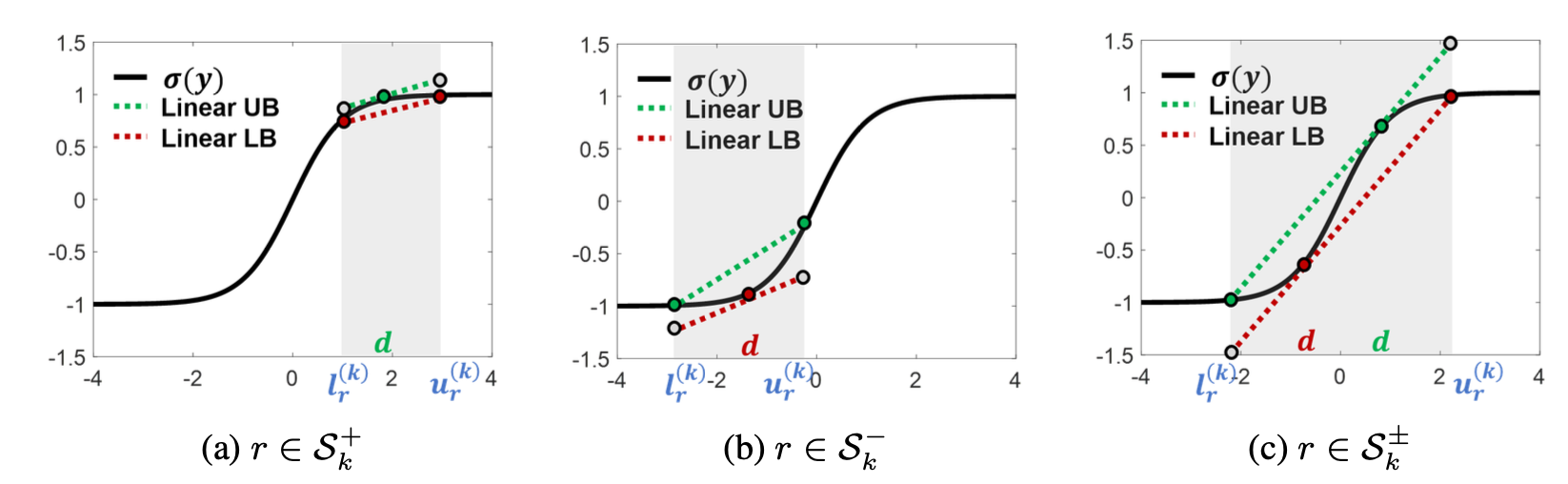
CROWN在Fast-Lin只作用于ReLU激活函数松弛基础上提出任何激活函数只要能被线性约束上下界或者二次函数约束上下界,那都可以通过松弛计算其鲁棒性,松弛方式如图4.3所示。
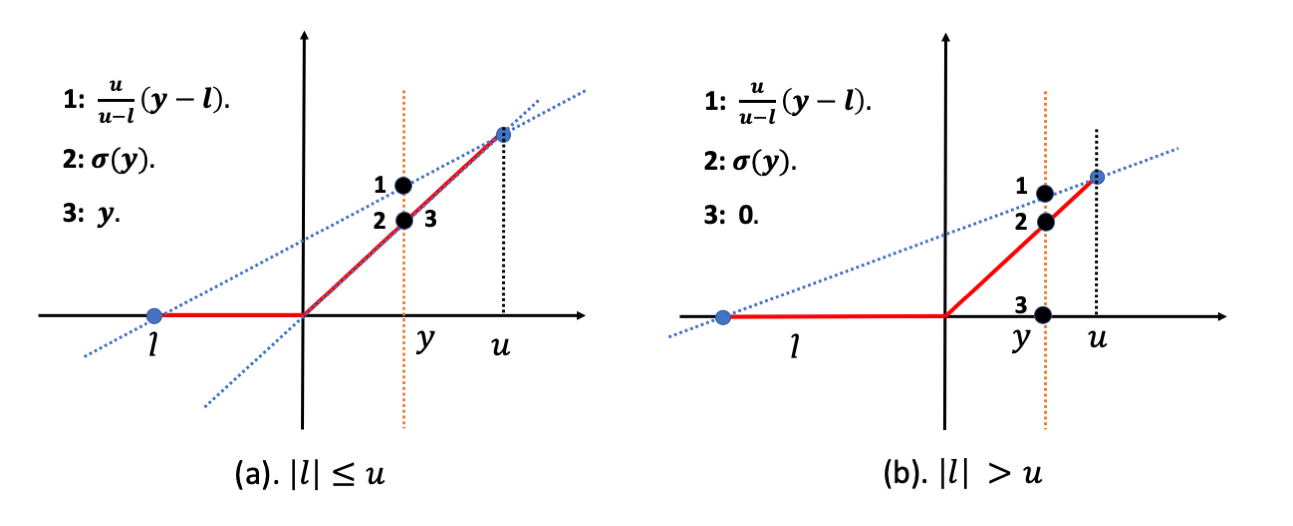
与Fast-Lin不同,CROWN允许灵活选择激活函数的上下界,从而实现有助于减少近似误差的自适应方案。以ReLU为例,CROWN提出以下松弛:
\[ay \leq \sigma(y) \leq \frac{u}{u-l}(y-l), \quad 0\leq a \leq 1\]当$a=\frac{u}{u-l}$时,即为Fast-Lin。当$|l| \leq u$ 时,取$a=1$。当$u \lt |l|$时,取a=0。如图4.4所示。
4.2 训练方法
(1)IBP
可以通过IBP松弛来获取最后一层输出上下界,从而第三章中损失函数来优化模型鲁棒性。
(2)CROWN-IBP
由于IBP松弛界限更加宽松,尤其是在训练开始时,它可能会遇到稳定性问题。所以提出了一种新的经过认证的对抗训练方法CROWN-IBP,当输入激活函数的上下界都为正或都为负时,用IBP方法传播边界。当输入激活函数值的上下界有正有负时,通过CROWN计算上下界。CROWN-IBP计算效率高,在训练可验证的强大神经网络方面始终优于IBP基线。
Reference
(1) IBP: https://arxiv.org/abs/1810.12715
(2) Fast-Lin,Fast-Lip:https://arxiv.org/abs/1804.09699
(3) CROWN: https://arxiv.org/abs/1811.00866
(4) CROWN-IBP: https://arxiv.org/abs/1906.06316
如果你觉得本文对你有帮助,不妨请我喝杯咖啡

